Materi 5 Matriks

Hay guys, apa kabar?  bertemu lagi kita 😊 masih ingat tentang materi 4 kemarin? Nah kali ini kita akan membahas tentang matriks. Masih ingat kan materi yang sudah dipelajari di smp dan smk/sma ini😊 mari kite mengulang dan pelajari lagi. Selamat belajar 😉😊

MATRIKS

1. Definis Matriks

Matriks adalah susunan beberapa bilangan dalam bentuk persegi Panjang yang diatur menurut baris dan kolom. Matriks dalam matematika merupakan kumpulan bilangan, simbol atau ekspresi berbentuk persegi panjang yang disusun menurut baris dan kolom. Bilangan-bilangan yang terdapat pada suatu matriks disebut dengan elemen atau disebut juga anggota dari suatu matriks. Contoh matriks dengan 2 baris dan 3 kolom yaitu sebagai berikut

Matriks banyak dimanfaatkan untuk menyelesaikan berbagai permasalahan matematika misalnya dalam menemukan solusi masalah persamaan linear, transformasi linear yakni bentuk umum dari fungsi linear contohnya rotasi dalam 3 dimensi. Matriks juga seperti variabel biasa, sehingga matrikspun dapat dimanipulasi misalnya dikalikan, dijumlah, dikurangkan, serta didekomposisikan. Menggunakan representasi matriks, perhitungan dapat dilakukan dengan lebih terstruktur.

2. Ordo Matriks

·         Ordo matriks adalah banyak baris dan kolom pada suatu matriks.

·         Matriks Am x n  menyatakan bahwa ordo matriks A adalah (m x n)

·         Matriks Am x n adalah suatu matriks yang terdiri atas m baris dan n kolom.

3.  OPERASI PADA MATRIKS

·         Penjumlahan
Penjumlahan matriks hanya dapat dilakukan terhadap matriks-matriks yang mempunyai ukuran (orde) yang sama. Jika A=(aij) dan B=(bij) adalah matriks-matriks berukuran sama, maka A+B adalah suatu matriks C=(cij) dimana (cij) = (aij)+(bij) atau [A]+[B] = [C] mempunyai ukuran yang sama dan elemennya (cij) = (aij) + (bij)

Contoh:

Contoh Soal:

·         Pengurangan

Sama seperti pada penjumlahan matriks, pengurangan matriks hanya dapat dilakukan pada matriks-matriks yang mempunyai ukuran yang sama. Jika ukurannya berbeda maka matriks hasil tidak terdefinisikan. Ditulis dengan A – B

Contoh:

Contoh soal:

·         Perkalian

Perkalian matriks dilakukan dengan cara tiap baris dikalikan dengan tiap kolom, selanjutnya dijumlahkan pada kolom yang sama.

Dua matriks, matriks A dan matriks B dapat dikalikan jika banyak kolom matriks A sama dengan banyak baris matriks B. Jika ordo matriks A adalah (m x n) dan ordo matriks B adalah (n x p), maka ordo matriks AB adalah (m x p).

Contoh:

Jika ordo matriks A adalah (3 x 2) dan ordo matriks B adalah (2 x 3), maka ordo matriks AB adalah (3 x 3)

Contoh soal:

Beberapa hal yang perlu diperhatikan:

1.      Perkalian matriks dengan matriks umumnya tidak komutatif

2.      Syarat perkalian adalah jumlah banyaknya kolom pertama matriks sama dengan jumlah banyaknya baris matriks kedua

4. Jenis – Jenis Matriks

A.    Matriks baris, adalah matriks yang terdiri atas satu baris .

            P_{1 x n} = (a_11, a₁₂ . . .  a₁₃)

B.     Matriks kolom, adalah matriks yang terdiri atas satu kolom.

    

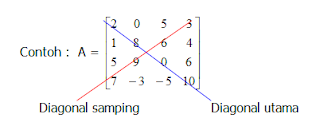
C.     Matriks persegi, adalah matriks dengan banyak baris sama dengan banyak kolom.

        

   

D.    Matriks identitas (i), adalah matriks persegi yang elemen-elemen pada diagonal utamanya adalah satu dan elemen lainnya adalah nol.

E.     Matriks transpos, adalah matriks dengan elemen-elemen pada baris diubah menjadi kolom atau sebaliknya.

Contoh: